Stolt偏移和Gazdag相移法的编程实现
地球物理

Stolt偏移和Gazdag相移法的编程实现

简单介绍Stolt偏移和Gazdag相移法流程以及其编程实现

Stolt偏移和Gazdag相移法均是地震偏移的方法，此处仅展示相关程序的实现。

准备工作

构造信号

# 生成Ricker子波
def ricker(f, length, dt):
    t = np.arange(-length / 2, (length / 2) + dt, dt)
    y = (1 - 2 * (np.pi ** 2) * (f ** 2) * (t ** 2)) * np.exp(-(np.pi ** 2) * (f ** 2) * (t ** 2))
    return t, y

# 设置Ricker子波参数
f = 50 # 子波频率
length = 0.04  # 子波长度
dt = 0.0005  # 采样间隔

t, wavelet = ricker(f, length, dt)
peak_index = np.argmax(wavelet) 
# 绘制子波
plt.plot(t, wavelet)
plt.title("Ricker子波")
plt.xlabel("时间 (s)")
plt.ylabel("振幅")
plt.show()

构造自激自收剖面

recenum=201 #接收器数量
timelen=2 #采样时间
vspeed=200#波速
receiver_len=200 #接收器长度
receivers = np.linspace(0, receiver_len, recenum)  # 接收器位置
dx=receivers[1]-receivers[0]
t=np.linspace(0,timelen,int(timelen/dt+1)) #时间轴

seismic_data = np.zeros((len(receivers), int(timelen/dt+1)))

for i, r in enumerate(receivers):
    # 假设绕射点位置固定在地下某点，这里为x=1000m，z=500m
    diffraction_x = 100
    diffraction_z = 50
  
    time_delay = np.sqrt((r - diffraction_x)**2 + diffraction_z**2)*2 / vspeed
    # 将时间延迟转换为样本点索引
    time_sample = int(time_delay / dt+1)
    start_idx = max(0, time_sample - peak_index)
    end_idx = min(seismic_data.shape[1], start_idx + len(wavelet))

    wavelet_start = 0
    wavelet_end = end_idx - start_idx
    if wavelet_end>=0:
        seismic_data[i, start_idx:end_idx] = wavelet[wavelet_start:wavelet_end]

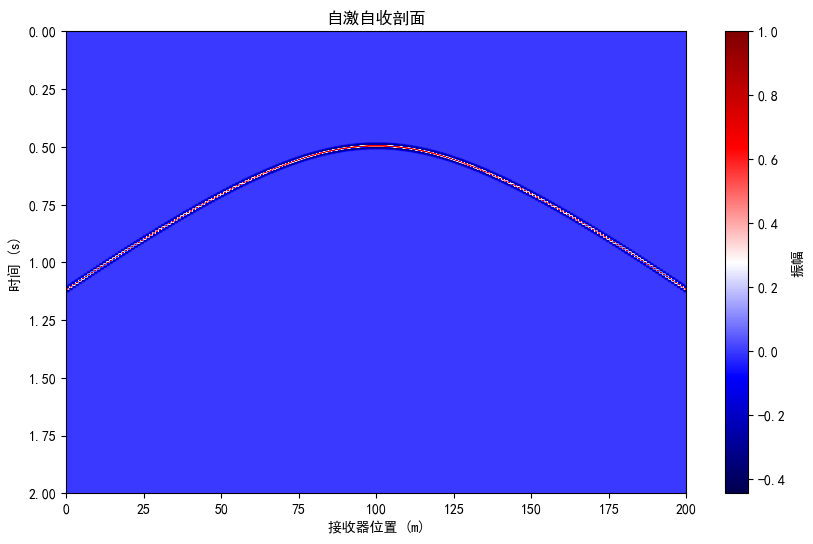
# 绘制剖面
plt.figure(figsize=(10, 6))
plt.imshow(seismic_data.T, extent=[0,receiver_len, timelen, 0], aspect='auto', cmap='seismic')
plt.colorbar(label='振幅')
plt.title('自激自收剖面')
plt.xlabel('接收器位置 (m)')
plt.ylabel('时间 (s)')
plt.show()
seismic_data=seismic_data.T

stolt偏移

stolt偏移的主要流程为：

  1. 对地震波进行二维傅里叶变换u(x,z=0,t)->u(k_x,z=0,\omega)

  2. 根据k_z=\sqrt{\frac{4\omega^2}{v^2}-k_x^2}进行从\omega映射到k_z,此处需要进行插值。u(k_x,z=0,\omega)->u(k_x,z=0,k_z)

  3. 加权u`(k_x,z=0,k_z)=u(k_x,z=0,k_z)*\frac{vk_z}{2\sqrt{k_x^2+k_z^2}}

  4. 二维傅里叶逆变换u`(k_x,z=0,k_z)->u(x,z,0)

代码实现过程中遇见很多问题，主要就是插值没插对，至少现在结果是好的,实现代码：

# Step 1: 傅立叶变换
n_time_points,n_traces = seismic_data.shape
u_kx_omega = fft2(seismic_data)
kx = fftfreq(n=n_traces, d=dx)
omega = fftfreq(n=n_time_points, d=dt)

# 只保留正频率
u_kx_omega = u_kx_omega[0:int(n_time_points/2)+1, :]
omega = omega[:int(n_time_points/2)+1]
Kx, Omega = np.meshgrid(kx, omega)

# Step 2: 频率-波数域映射到 k_z
k_z_squared = 4 * (Omega**2) / (vspeed**2) - Kx**2
k_z_squared = np.maximum(k_z_squared, 0)
Kz = np.sqrt(k_z_squared)

# 插值到 (kx, kz) 网格
kz_target = np.linspace(np.min(Kz), np.max(Kz), len(omega))
KX, KZ = np.meshgrid(kx, kz_target)
# 二维插值
points = np.column_stack((Kx.flatten(), Kz.flatten()))
values = u_kx_omega.flatten()
u_kx_kz = griddata(points, values, (KX, KZ), method='linear', fill_value=0)

# 加权因子
offset_factor = KZ * vspeed / (2 * np.sqrt(KZ**2 + KX**2))
offset_factor = np.nan_to_num(offset_factor) 

# Step 3: 加权
u_kx_kz *= offset_factor
# Step 4: 逆傅立叶变换
u_xz = np.real(ifft2(u_kx_kz, s=(len(omega), n_traces)))



#绘图
z = np.linspace(0, len(omega) * dt * vspeed, len(omega))
x = np.arange(n_traces) * dx
#平均值归一化
u_xz = (u_xz - np.mean(u_xz)) / np.max(np.abs(u_xz))

plt.figure(figsize=(20, 10))
plt.imshow(u_xz, extent=[0, receiver_len, timelen*vspeed/2, 0],aspect='auto', cmap='seismic', vmin=-1, vmax=1)
plt.colorbar(label='振幅')
plt.title('stolt')
plt.xlabel('接收器位置 (m)')
plt.ylabel('深度 (m)')
plt.show()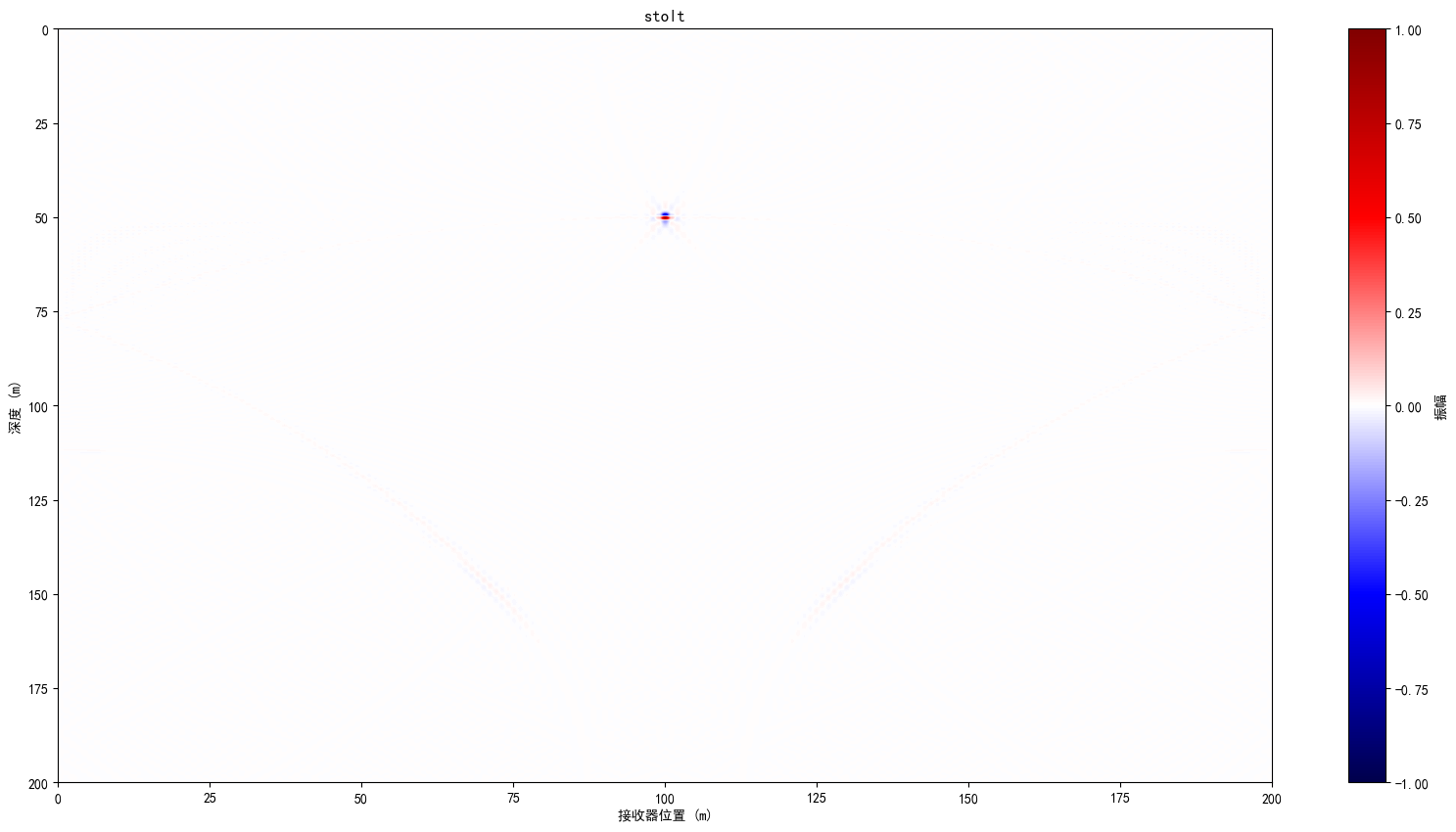

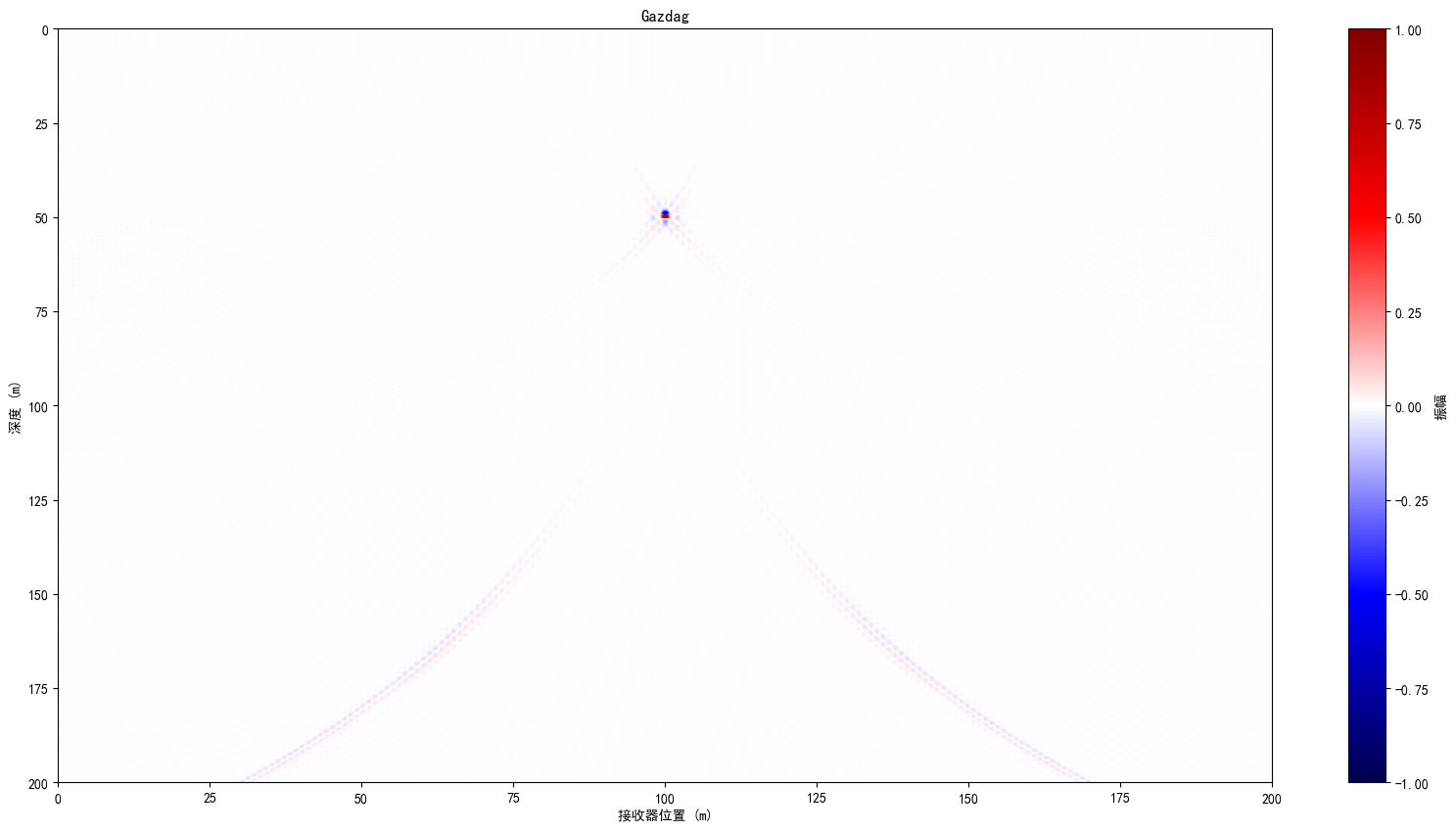
Gazdag相移法

Gazdag相移法主要流程：

  1. 对地震波进行二维傅里叶变换u(x,z=0,t)->u(k_x,z=0,\omega)

  2. 利用相移算子e^{i\Delta zk_z}进行向下延拓,其中k_z=\sqrt{\frac{4\omega^2}{v^2}-k_x^2}，u(k_x,z+\Delta z,\omega)=e^{(i\Delta zk_z)}u(k_x,z,\omega)，此处计算k_z的速度应该是z对应层的速度，但是我的模型没有速度分层就不考虑了。

  3. 相加所有频率，进行一维傅里叶逆变换u(k_x,z+\Delta z,\omega)->u(x,z+\Delta z,t=0)

  4. 重复2，3步，获得偏移后的剖面

实现代码有点问题，可能是没理解好，不知道为什么相移算子再乘\pi,才能获得正确的偏移位置，不然虽然收敛绕射波但是位置不对，代码实现：

delta_z=1#深度间隔
u_xz=[]#存储波场
# Step 1: 傅立叶变换
n_time_points,n_traces = seismic_data.shape
u_kx_omega = fft2(seismic_data)
kx = fftfreq(n=n_traces, d=dx)
omega = fftfreq(n=n_time_points, d=dt)
# 只保留正频率
u_kx_omega = u_kx_omega[0:int((n_time_points+1)/2), :]
omega = omega[:int((n_time_points+1)/2)]
Kx, Omega = np.meshgrid(kx, omega)
# Step 2: 计算kz
k_z_squared =(2*Omega)**2 / (vspeed**2) - Kx**2
k_z_squared = np.maximum(k_z_squared, 0)
Kz = np.pi*np.sqrt(k_z_squared)

for i in np.arange(0,vspeed*timelen/delta_z+delta_z,delta_z):
    #Step2:向下延拓
    u_kx_omega=np.exp(1j*delta_z*Kz)*u_kx_omega
    #Step3:逆傅立叶变换
    u_kx_z=np.sum(u_kx_omega,axis=0).T
    u_xz.append(ifft(u_kx_z))
#绘图
u_xz=np.array(u_xz)
u_xz=np.real(u_xz)
#归一化
u_xz = (u_xz - np.mean(u_xz)) / np.max(np.abs(u_xz))
plt.figure(figsize=(20, 10))
plt.imshow(u_xz, extent=[0, receiver_len, timelen*vspeed/2, 0],aspect='auto', cmap='seismic', vmin=-1, vmax=1)
plt.colorbar(label='振幅')
plt.title('Gazdag')
plt.xlabel('接收器位置 (m)')
plt.ylabel('深度 (m)')
plt.show()

Comment
:moonhoro